Statistik merupakan ilmu yang berkaitan dengan pengumpulan, pengolahan, analisis, interpretasi, dan presentasi data. Dalam kehidupan sehari-hari, kita sering kali dihadapkan dengan berbagai data yang perlu dipahami dan dianalisis. Statistik membantu kita menggali makna dan pola dari data tersebut.
Dengan menggunakan metode dan teknik statistik, kita dapat menjawab pertanyaan-pertanyaan yang relevan, membuat keputusan yang lebih informasional, dan mengidentifikasi tren atau pola yang dapat memberikan wawasan baru. Statistik digunakan secara luas dalam berbagai bidang, termasuk ekonomi, ilmu sosial, kesehatan, sains, dan bisnis.
Konsep mean, median, modus memiliki peran penting dalam statistik sebagai ukuran tendensi sentral atau pusat data. Pemahaman tentang konsep mean, median, dan modus memungkinkan kita untuk menganalisis dan memahami karakteristik data yang kita hadapi.
Masing-masing ukuran ini memberikan wawasan yang berbeda tentang bagaimana data tersebar atau terpusat.
Dalam artikel ini kita akan belajar mengenai perbedaan mean median modus tersebut.
Daftar Isi
Apa Itu Mean Median Modus?
Dalam interpretasi statistik, kita sering kali menggunakan mean median modus ini secara bersama-sama untuk mendapatkan pemahaman yang lebih lengkap tentang data.
Dengan memahami konsep ini, kita dapat mengambil keputusan yang lebih baik, membuat prediksi yang lebih akurat, dan menyajikan informasi yang lebih relevan berdasarkan data yang kita miliki. Oleh karena itu, pemahaman tentang mean, median, dan modus adalah sangatlah penting dalam memahami dan menerapkan statistik ataupun pengukuran di berbagai bidang.
Simak Juga : Pengertian Pengukuran Dalam Ilmu Fisika Beserta Contohnya
-
Mean
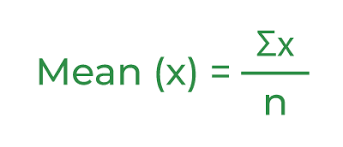
Mean, atau yang sering disebut sebagai rata-rata, adalah salah satu ukuran tendensi sentral yang paling umum digunakan dalam statistik. Mean adalah hasil dari penjumlahan semua nilai dalam suatu himpunan data, kemudian hasil penjumlahan tersebut dibagi dengan jumlah data yang ada.
Secara intuitif, mean dapat dianggap sebagai nilai tengah atau representatif dari sekumpulan data.
Rumus Perhitungan Mean
Rumus perhitungan mean adalah sebagai berikut:
Mean = (x₁ + x₂ + x₃ + … + xn) / n
Dalam rumus di atas, x₁, x₂, x₃, dan xn merupakan nilai-nilai individu dalam himpunan data, sedangkan n adalah jumlah total data yang ada dalam himpunan tersebut.
Contoh penggunaan mean dalam statistik

Misalkan kita memiliki data tinggi badan siswa di sebuah kelas, yaitu 160 cm, 165 cm, 170 cm, 155 cm, dan 175 cm.
Untuk mencari mean atau rata-rata tinggi badan siswa, kita menjumlahkan semua nilai tersebut :
160 + 165 + 170 + 155 + 175 = 825
Selanjutnya, kita bagi jumlah tersebut dengan jumlah data, yaitu 5.
Sehingga, mean tinggi badan siswa dalam kelas tersebut adalah 825 / 5 = 165 cm.
Dengan menggunakan mean, kita dapat menggambarkan tinggi badan rata-rata dari seluruh siswa di kelas tersebut
Kelebihan dan kelemahan penggunaan mean
Kelebihan penggunaan mean adalah sebagai berikut :
-
- Mean adalah ukuran yang paling umum dan mudah dipahami.
- Mean dapat digunakan untuk melakukan perbandingan antara beberapa himpunan data.
- Mean memiliki sifat matematis yang memudahkan dalam penggunaan dalam berbagai analisis statistik.
Namun, ada beberapa kelemahan yang perlu diperhatikan dalam penggunaan mean :
-
- Mean tidak cocok untuk digunakan jika data tidak memiliki distribusi yang simetris atau normal. Jika distribusi data tidak merata, mean mungkin tidak mewakili pusat data dengan baik.
- Mean tidak cocok digunakan jika data mengandung data kategorikal atau data ordinal.
- Mean sangat sensitif terhadap pencilan (outlier) dalam data. Pencilan yang ekstrem dapat mempengaruhi nilai mean secara signifikan, sehingga tidak merefleksikan secara akurat keadaan sebagian besar data.
Dalam pemilihan ukuran tendensi sentral, perlu dipertimbangkan karakteristik data dan tujuan analisis yang ingin dicapai. Jika data memiliki outlier yang signifikan atau distribusi yang tidak normal, alternatif lain seperti median atau modus dapat dipertimbangkan untuk memberikan gambaran yang lebih akurat tentang data.
Simak Juga : Outlier Pada Uji Profisiensi bagi Laboratorium Pengujian
-
Median

Median adalah salah satu ukuran tendensi sentral dalam statistik yang digunakan untuk menentukan nilai tengah dalam suatu himpunan data.
Dalam proses perhitungannya, data diurutkan dari yang terkecil hingga yang terbesar, kemudian nilai tengahnya diambil sebagai median. Median adalah nilai yang membagi data menjadi dua bagian yang sama, di mana setengah nilai berada di atasnya dan setengah nilai berada di bawahnya.
Rumus Perhitungan Median
Untuk menghitung median, langkah-langkah yang harus dilakukan adalah sebagai berikut:
-
- Urutkan data dalam urutan menaik
- Jika jumlah data ganjil, median adalah nilai tengah dari data yang telah diurutkan.
- Jika jumlah data genap, median adalah nilai rata-rata dari dua nilai tengah setelah data diurutkan.
Contoh penggunaan median dalam statistik
Misalkan terdapat himpunan data berikut untuk jumlah poin yang diperoleh dalam sebuah ujian :
70, 85, 65, 80, 75
Langkah pertama adalah mengurutkan data secara menaik : 65, 70, 75, 80, 85
Karena jumlah data ganjil, median adalah nilai tengah, yaitu 75.
Dengan menggunakan median, kita dapat mengetahui bahwa setengah dari siswa memiliki nilai di atas 75 dan setengah siswa lainnya memiliki nilai di bawah 75
Kelebihan dan kelemahan penggunaan median
Kelebihan penggunaan median adalah sebagai berikut :
-
- Median tidak terpengaruh oleh adanya outlier atau pencilan yang signifikan dalam data. Hal ini membuat median lebih stabil daripada mean dalam situasi di mana ada data ekstrem yang dapat mempengaruhi hasil secara drastis.
- Median dapat digunakan pada data dengan distribusi yang tidak simetris atau tidak normal.
- Median memberikan gambaran yang lebih baik tentang nilai tengah ketika terdapat ketimpangan dalam distribusi data.
Namun, terdapat beberapa kelemahan yang perlu diperhatikan dalam penggunaan median:
-
- Median kurang sensitif terhadap variasi dalam data. Ketika ada variasi yang signifikan di antara nilai-nilai di dalam data, median mungkin tidak memberikan informasi yang cukup detail tentang sebaran data.
- Perhitungan median memerlukan proses pengurutan data, yang dapat memakan waktu dan sumber daya komputasi yang lebih besar daripada menghitung mean.
- Median tidak memberikan informasi tentang proporsi relatif data di sekitar nilai median.
Dalam penggunaan median, penting untuk mempertimbangkan karakteristik data serta tujuan analisis yang ingin dicapai. Jika data memiliki outlier yang signifikan atau distribusi yang tidak simetris, median dapat menjadi ukuran tendensi sentral yang lebih cocok daripada mean.
-
Modus

Modus adalah nilai atau nilai-nilai dalam suatu himpunan data yang paling sering muncul. Dalam kata lain, modus adalah nilai yang memiliki frekuensi tertinggi dalam data. Konsep modus digunakan untuk mengidentifikasi nilai dominan atau paling umum dalam data.
Rumus perhitungan modus
Rumus perhitungan modus cukup sederhana. Untuk mencari modus, kita harus mengidentifikasi nilai atau nilai-nilai yang memiliki frekuensi tertinggi dalam himpunan data.
Jika hanya ada satu nilai yang muncul paling sering, maka nilai itu adalah modus tunggal. Namun, jika ada lebih dari satu nilai dengan frekuensi tertinggi yang sama, maka data memiliki modus ganda atau banyak modus.
Contoh penggunaan modus dalam statistik
Misalkan kita memiliki data tinggi siswa dalam sebuah kelas, yaitu :
160 cm, 165 cm, 170 cm, 155 cm, 165 cm, dan 175 cm
Untuk mencari modus atau nilai yang paling sering muncul, kita melihat frekuensi kemunculan setiap nilai.
Dalam contoh ini, nilai 165 cm muncul sebanyak 2 kali, sementara nilai lainnya muncul hanya 1 kali.
Oleh karena itu, modus dari data ini adalah 165 cm.
Dengan menggunakan modus, kita dapat mengidentifikasi tinggi yang paling umum atau paling dominan di antara siswa-siswa dalam kelas tersebut
Kelebihan dan kelemahan penggunaan modus
Kelebihan penggunaan modus adalah sebagai berikut :
-
- Modus memberikan informasi langsung tentang nilai yang paling sering muncul dalam data.
- Modus dapat digunakan pada data kategorikal atau data ordinal yang tidak memiliki hubungan matematis.
Namun, terdapat beberapa kelemahan yang perlu diperhatikan dalam penggunaan modus :
-
- Jika data memiliki variasi frekuensi yang signifikan atau distribusi yang merata, modus mungkin tidak memberikan gambaran yang cukup representatif tentang pusat data secara keseluruhan.
- Modus tidak dapat digunakan pada data kontinu karena modus hanya memberikan nilai-nilai diskrit yang ada dalam data.
- Jika semua nilai dalam data muncul dengan frekuensi yang sama, maka data tersebut tidak memiliki modus.
Dalam pemilihan ukuran tendensi sentral, perlu dipertimbangkan karakteristik data serta tujuan analisis yang ingin dicapai. Modus cocok digunakan ketika kita ingin mengetahui nilai yang paling sering muncul dalam data atau untuk data kategorikal yang tidak memiliki nilai numerik. Namun, perlu diingat bahwa modus dapat memberikan gambaran yang terbatas dan tidak memberikan informasi yang detail tentang sebaran data.
Kesimpulan

Pemahaman tentang mean, median, dan modus merupakan hal penting dalam statistik maupun pengukuran karena parameter tersebut adalah ukuran tendensi sentral yang memberikan informasi tentang nilai-nilai pusat dalam suatu himpunan data.
Mean, median, dan modus memberikan gambaran yang berbeda tentang data dan masing-masing memiliki kegunaannya sendiri tergantung pada sifat data dan tujuan analisis.
Mean digunakan untuk menggambarkan rata-rata aritmatika data, median digunakan untuk mengidentifikasi nilai tengah yang tidak dipengaruhi oleh nilai ekstrem, dan modus digunakan untuk mengidentifikasi nilai yang paling sering muncul.
Memahami ketiga ukuran ini membantu dalam menginterpretasikan data dengan lebih baik dan membuat keputusan yang lebih tepat dalam analisis statistik.
Dalam prakteknya, penggunaan yang tepat dari mean, median, dan modus dapat membantu mengungkap pola-pola, mengidentifikasi outlier, dan memberikan gambaran yang lebih lengkap tentang data yang sedang dianalisis.
Buat anda yang bekerja di laboratorium jasa kalibrasi pemahaman ini (terutama perhitungan mean atau rata-rata) juga sangat penting karena terkait dengan perhitungan estimasi ketidakpastian pengukuran dari hasil kalibrasi tersebut.
Semoga Bermanfaat.






